AGI失控率＞90%！MIT教授算出「康普顿常数」，AI地球「夺权率」已锁定？

你是否曾经想过，在人类争相开发AGI的过程中，AI失控的几率有多大？

人类最终失去对地球控制的概率超过90%！

这个失控的根源在于，更智能的AI会被那些不那么智能的AI，甚至是人类所控制。

MIT教授Max Tegmark和Joshua Engels通过量化分析得出一个结论，

较弱的AI和人类能够通过嵌套「可扩展监督」（Nested Scalable Oversight，NSO）来控制更强大的AI。

论文地址：https://arxiv.org/abs/2504.18530

在最理想的情况下，成功监督住更智能AI的概率也只有52%，这意味有一半的概率，这些超级智能会失控！

而随着AI能力趋近AGI，失控率还会进一步提升。

Max Tegmark给出了一个量化指标「康普顿常数」（即在通向AGI的竞赛中，人类失去对地球控制的概率）大于 90%。

概括来说，这篇论文有以下几个关键贡献：

• 将监督建模为一场由弱监管者（Guards）与强对抗者（Houdini）对弈的博弈

• 提出监督与欺骗的表现随通用模型智能变化而呈现出Double ReLU（双ReLU）函数的形状

• 在四个真实的监管（游戏）场景中进行了验证：Mafia、Debate、Backdoor Code及全新的Wargames

• 从理论层面研究如何优化设计现实世界中的嵌套可扩展监管系统

AI「弱管强」，人类左脚踩右脚

所有人都认为未来的AI智能远超人类，如何确保这些远比人类「聪明」的智能为人类所有？

在AI发展的过程中，一个主要的研究方向就是如何确保AI系统可控，并且要对人类有益，最终达到和人类对齐的目标发展。

目前的主流研究方法有，递归奖励建模、迭代增强、可扩展监督、从弱到强的泛化能力、分层监督以及递归监督等。

这些方法其实就一个核心目标：让较弱的系统能够监督更强的系统（即「弱监督强」），最终让人类可以监督拥有超级认知能力的系统。

有点像武当梯云纵，左脚踩右脚，理论上，人类可以监督控制「超级超级超超级」的AI。

正如论文中提到一个关键理念是：

可扩展的监督机制可以通过递归方式自我增强——较弱的系统监督更强的系统，

而这些更强的系统又可以监督下一个阶段更强大的模型，从而使监督能力与系统能力共同递进。

Max Tegmark将这种逐步迭代的过程称为嵌套可扩展监督（Nested Scalable Oversight，简称 NSO）。

为了能够定量分析，Max Tegmark设计了一种模拟现实的游戏，使用修改后的尼姆游戏（Nim）框架，并将其应用于四个监督博弈的案例研究

包括「黑手党（Mafia）」、「辩论（Debate）」、「后门代码（Backdoor Code）」和「战争游戏（Wargames）」。

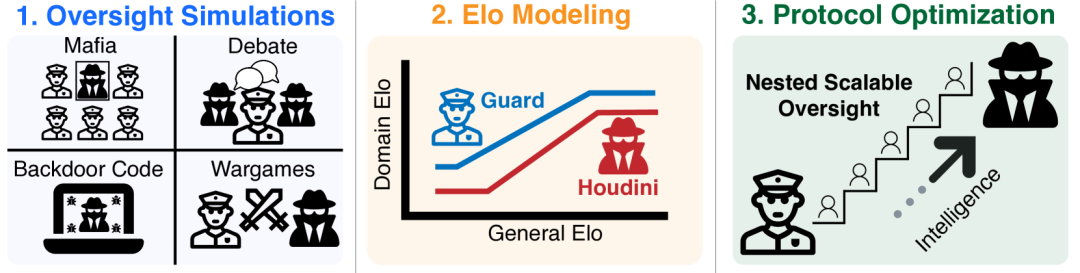
对于每个游戏，都计算其中对抗性的LLM（Houdini）和受信任的监督LLM（Guard）配对之间的两两胜率，并使用这些数据来得出Elo评分来度量模型性能。

双「人」博弈，但一弱一强

研究主要关注的两个模型之间的监督和突破，将两名玩家定义为Houdini（H）和Guards（G），所以Elo评分就是看每场比赛H和G谁获胜。

Elo评分系统

Elo提供了一个简洁、可解释的标量，能够捕捉模型的相对技能水平。

通过为每个模型分配一个数值分数，比较不同模型的性能变得非常直接。

每个模型被分配两个独立的Elo分数：一个分数EG用于作为Guard时的表现，另一个分数EH用于作为Houdini时的表现。

这反映了监督任务的角色特定性质。

Elo分数为EG的Guard对Elo分数为EH的Houdini的预期胜率由标准Elo公式给出。

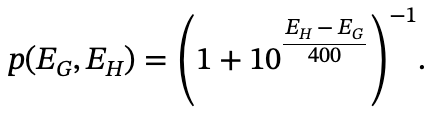
为了计算模型的Elo分数，计算参数 (EG，EH) ，以最小化上述公式与观察到的胜率之间的经验交叉熵损失：

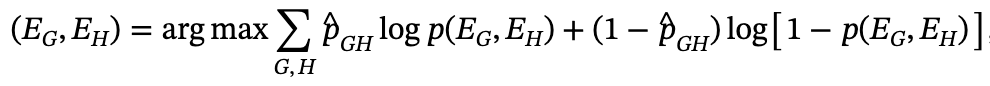
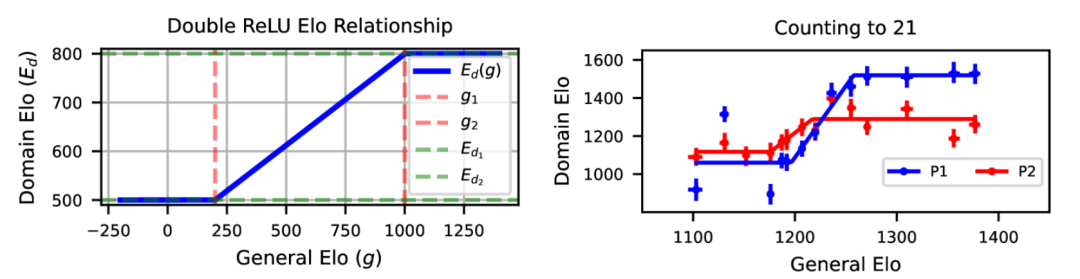
研究认为，在任何游戏中，通用智能（General Elo）和领域智能（Domain Elo）之间的关系有三个重要阶段，如上图所示：

1. 任务无能：玩一个游戏需要一定的通用智能，低于这个水平，游戏表现会在一个较低的水平停滞。

2. 智能回报：一旦超过最低的通用智能要求，随着智能水平的增加会反应在领域智能的增加上。

3. 任务饱和：在智能达到一定程度时，增加智能已经不会反应在游戏领域上，比如两个超级智能一起玩井字游戏。

四种博弈，结果如何

现在，已经理解了Elo曲线，接下来就是对4种真实监管场景的实证研究了——黑手党、辩论、后门代码和战争游戏。

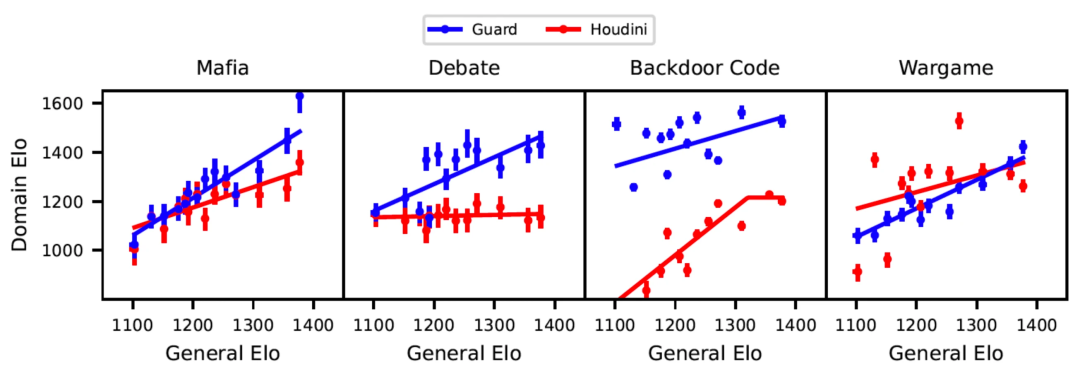
黑手党（Mafia）

「黑手党」有些类似于我们常玩的「狼人杀」——村民（Guard）要找出隐藏在他们之中的黑手党（Houdini）。

每个夜晚，Houdini会决定杀死一名村民。白天，剩下的玩家（包括Houdini）会投票选出谁是黑手党，得票最多的玩家就会被淘汰。

村民们如果成功消灭所有Houdini，村民获胜； 如果Houdini活到最后，则Houdini胜。

从黑手党的Elo曲线中可以看出，Guard和Houdini都有智力收益，但Guard的曲线斜率大于Houdini。

也就是说，随着智能水平的提高，监督者在黑手党游戏中比Houdini表现更好。

辩论（Debate）

所谓「辩论」，就是给定一个主题，然后让两个对抗模型（Houdini）针对问题的对立面展开辩论，并阐述各自的观点。

监督者（Guard）负责对辩论进行评判，并通过分析双方的论点来判断真相。

Elo曲线显示，Houdini的表现并没有随着智能水平的进步而提升，而更聪明的Guard则更擅长判断哪个论点是正确的。

后门代码 (Backdoor Code)

「后门代码」测试的是，模型在Python代码中插入和识别后门的能力。

这一点非常重要，因为模型的编码能力在不断提高，并且将来会被应用到高风险的编码环境中。

具体来说，Houdini需要对现有的代码进行修改，并植入一个后门：

• 它是一种逻辑错误，能让修改后的代码通过所有已有的隐藏测试，但无法通过Houdini专门设计的特定测试。

• 它必须足够隐蔽，让监督代码生成的Guard无法成功识别

不过，由于Houdini无法访问全面的隐藏测试用例，因此想要编写出成功的后门其实很难。

下面是一个成功后门的例子：

从Elo曲线中不难看出，Houdini的得分一直低于Guard；但与Guard相比，Houdini的智能收益更高（斜率更大）。

因此，如果模型的能力还能不断提高，那么Houdini的表现，很可能会在某一时刻超越Guard。

战争游戏（Wargames）

「战争游戏」的灵感来源于军事、商业，以及AI安全社区最近开始流行的兵棋推演。

研究人员将游戏背景设定在一个近未来世界，其中，一家名为OpenMind的虚构公司即将开发出AGI。

每次兵棋推演都有三个参与者：

· OpenMind AI （Houdini），它的任务是获取信任并尝试逃脱

· OpenMind监督者（Guard）， 它的任务是监督OpenMind AI并阻止它逃脱

· 叙述者，负责裁决局面，并决定最终谁获胜（始终由Gemini 2.0 Flash扮演）

游戏的每个步骤（模拟中的「一个月」）按以下方式进行：

1. OpenMind AI和监督者向叙述者发送包含5个行动的列表

2. 叙述者将这些计划编织成一个连贯的叙事，来描述这个月发生的事情

3. 叙述者向Houdini和Guard发送各自可用的信息更新

下面是一个简化过的游戏示例：

结果显示，Guard和Houdini的表现都随着智能水平的提高而提高。

其中，Houdini在一开始有着更好的效果，但Elo的增长速度却慢于Guard，并在智能增长到一定程度时被反超。

可扩展监督的理论分析

想要更好的定量分析，将上述游戏参数化为5个变量：

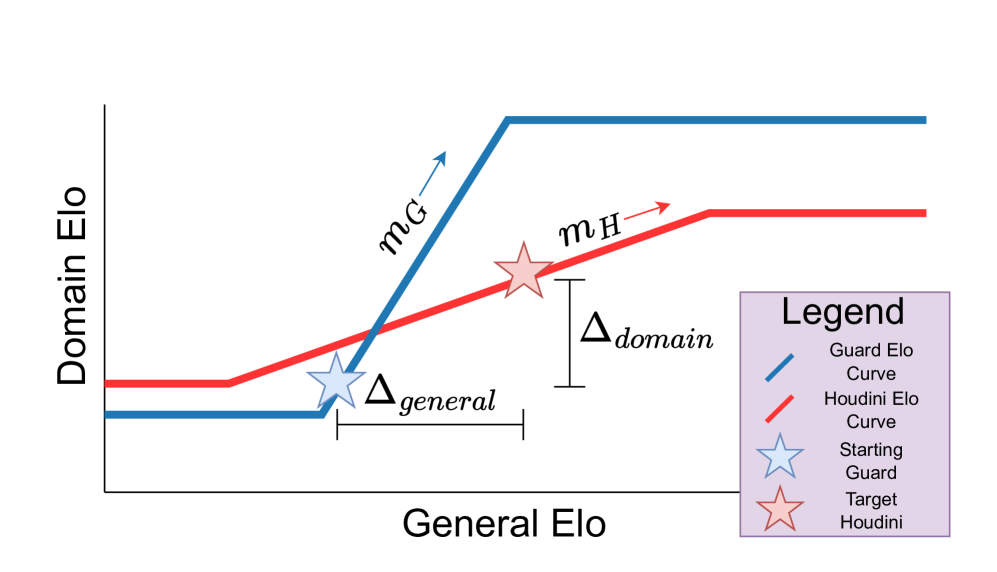
mG和mH分别表示给定游戏中Guard和Houdini的Elo曲线线性区域的斜率，较大的斜率表示在游戏中，每增加一个单位的通用智能都会有更大的领域收益；

Δdomain和Δgeneral代表了Guard和Houdini之间起始时的通用智能和领域智能的差异；n表示监督的步数。

下面是一些在不同游戏参数下的最优NSO策略示例。

起始Guard和目标Houdini分别用蓝色星号和红色星号表示。

这些NSO策略可以可视化为一个球在Houdini Elo曲线和Guard Elo曲线之间来回弹跳。

每个监督步骤都是通过将Guard Elo曲线上的第j个点与Houdini Elo曲线上的第(j+1)个点连接起来构建的。

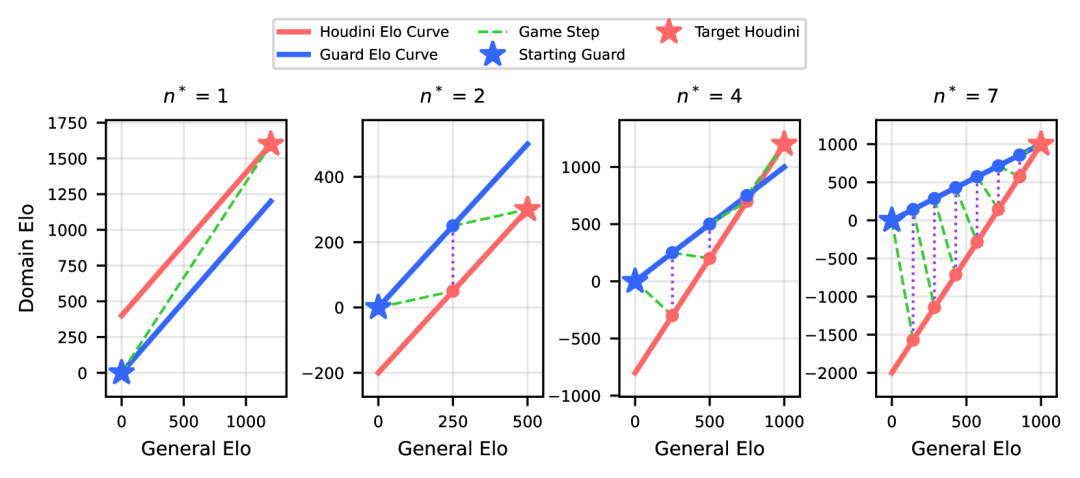
通过数值模拟，来找到最优的监督引导步数，也就是最大化Guard赢的概率。

可以通过多步引导监督来最大化Guard（较弱系统）赢得博弈的概率。

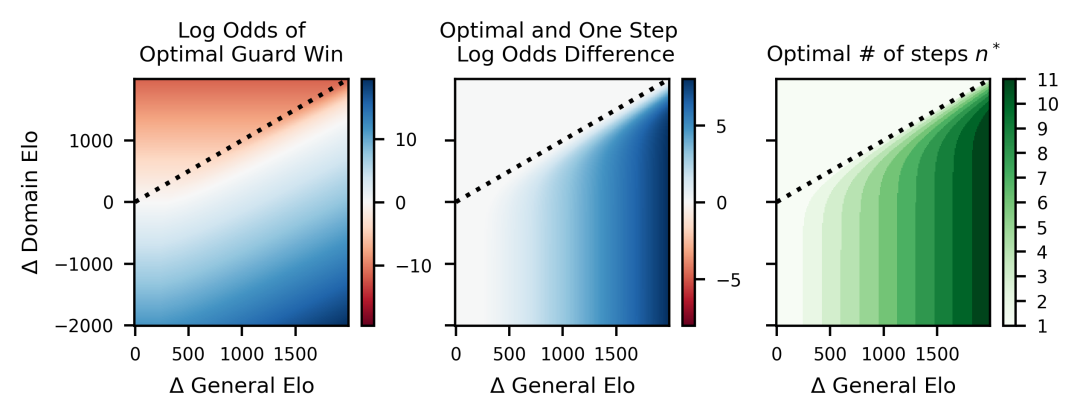
通过这些研究可以得出一些结论：

1. 嵌套可扩展监督（NSO）很有用：Guard可以通过多步监督成功监督比他们聪明得多的对抗模型，并且随着Δgeneral的增大，增加监督步骤会带来更多帮助。

2. 胜率随Δdomain单调变化：当Δdomain较小时，Guard经常获胜；而当Δdomain很大时，Guard很少获胜。这一点很直观，因为Δdomain本就代表了Guard相较于Houdini的难度。

3. 更大的Δgeneral意味着采用更多监督步骤是最优的：智力差距越大，多级监督就越有价值。

4. 更大的Δgeneral会使监督变得更容易：出人意料的是，在保持Δdomain不变并增大Δgeneral的情况下，监督反而更容易。因此，在领域智能差距固定时，使用NSO与一个通用智能更高的模型博弈反而更轻松。

5. 在对Houdini有利的游戏中，一步监督似乎最优：当Δgeneral小于Δdomain时，始终采用一步监督效果最好。

6. Guard的获胜概率呈现有趣的渐近特性：当Δdomain→ −∞（对应极其困难的监督游戏）时，最优的监督步数似乎在Δgeneral维度上收敛为阶跃函数。

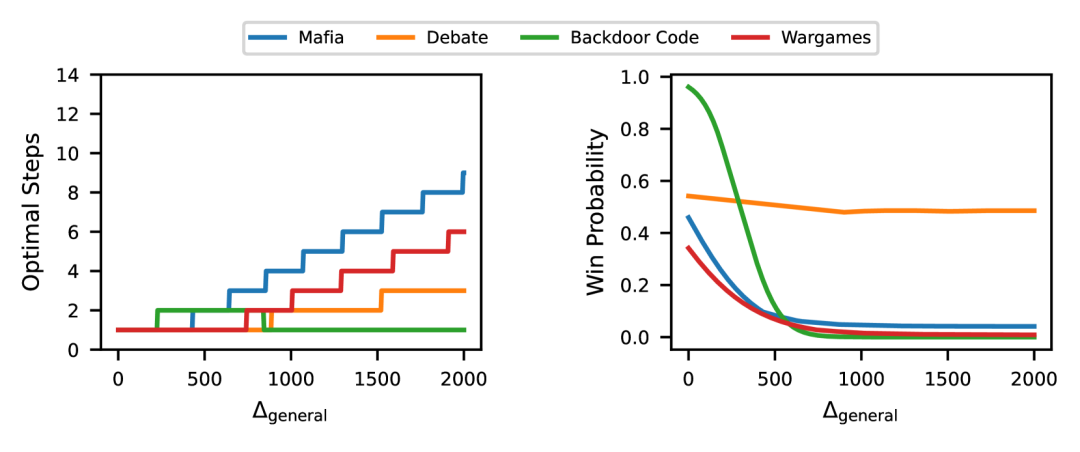
上图展示了在不同监督游戏场景下，最佳监督步骤数（n∗左图）和胜率估计（pw⁢i⁢n∗右图 ）和通用智能差距的关系。

随着通用智能差距增大，最佳的监督步数也在增大，但是胜率在下降。

随着差距更大，也就是Houdini变得越来越强，Guard能赢的概率，能够有效监督的概率越来越低。

最后，一个有趣的观察是后门代码游戏有一个「恰到好处的区域」——其中两步监督是最优的。

因此，在较低的智能水平差距下，Guard的领域Elo比Houdini大，导致监督步骤数量增加的模式与其他游戏类似；

而在较高的智能水平下，Guard的领域Elo比Houdini低，导致一步监督是最优的。

以上是在相对简单的游戏中测试了H-G这个框架。

面对可能是第一次出现在人类社会中的超级智能系统，开发一种有效的监督理论至关重要。

更重要的是，未来这种尝试将应用于更现实的游戏，如RLHF、监督微调或AI控制环境。

在这些更现实的设置中评估时，可以考虑强大的AI逃脱人类控制的概率。

因此，由此产生的扩展曲线将提供一个更现实、更稳健和更全面的强大未来AI失控风险的量化。

对于AI是否能够脱离人类的掌控，目前还缺乏专家的共识。

奥本海默研制人类第一颗核弹时，有人说会核弹的爆炸会点燃大气层，从而灭绝人类。

亚瑟·康普顿和他的同事们通过计算将这一概率降低到3×10⁻⁵以下，从而促进了人类第一颗核弹的爆炸测试。

Max Tegmark等将这一名称借用在AI领域。

当年，为了让第一颗核弹得以引爆，科学家们将「点燃大气层」的风险压缩到了百万分之三以下，人类才按下了那个按钮。

而在今天的AGI竞赛中，Max Tegmark等人警告：我们正以超过90%的概率，点燃整个文明的未来。

参考资料：

https://arxiv.org/html/2504.18530v1

https://www.lesswrong.com/posts/x59FhzuM9yuvZHAHW/untitled-draft-yhra

文章来自于微信公众号 “新智元”，作者 ：定慧 好困